Matematika je jasným a exaktným jazykom vedy. Neraz v sebe skrýva aj nečakané súvislosti a zaujímavé výsledky, ktoré pôsobia zvláštne, ba čarovne.
Existujú čísla, ktoré majú pri správnom použití matematických operácií špecifické vlastnosti. Či už ide o jednoduché sčítanie, odčítanie, násobenie a delenie, alebo o komplexnejšie a zložitejšie operácie. Prvým pekným príkladom je číslo 142 857. Keď ho vynásobíme ktorýmkoľvek jednociferným číslom od 1 do 6, jeho cifry ostanú rovnaké, dokonca v rovnakom poradí, iba sa o niekoľko miest posunú. Napríklad 142 857 × 4 = 571 428.
Číslo 1 034 482 758 620 689 655 172 413 793 má zasa tú vlastnosť, že keď ho vynásobíme číslom 3, výsledok tvoria tie isté cifry iba s malou zmenou, a to presunutie číslice 3 z konca na začiatok.
Číslo 73
Hoci je číslo 73 nízke, má mnoho zaujímavých vlastností. Číslo, ktoré je bez zvyšku deliteľné iba jednotkou a samým sebou, nazývame prvočíslo. Číslo 73 je 21. prvočíslo v poradí, zatiaľ čo jeho zrkadlová forma, číslo 37, je 12. prvočíslo v poradí, čo je zrkadlová forma čísla 21. Navyše súčin 7 × 3 = 21.
V dvojkovej sústave, v ktorej sa používajú iba číslice 0 a 1, sa číslo 73 vyjadrí ako 1001001, čo je palindróm, teda rovnaké číslo pri čítaní číslic zľava aj sprava. A v osmičkovej sústave ho zapíšeme ako 111.
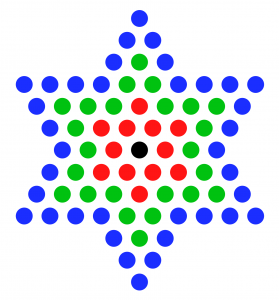
Čísla 73 a 37 majú aj ďalšie prepojenia. Sú to po sebe idúce tzv. hviezdne čísla. Ide o počet potrebných bodiek pri vytvorení šesťcípej hviezdy. Okolo jednej bodky sa pravidelne umiestni 13 bodiek, čo vytvorí najmenšiu možnú hviezdu. Následne ďalších práve 37 bodiek okolo vytvorí väčšiu hviezdu a 73 opäť väčšiu.
Sú aj po sebe idúce šťastné prvočísla. Ako šťastné číslo sa neoznačuje iba číslo prinášajúce šťastie v kultúre. Pôvod šťastných čísel vznikol ako Eratostenovo sito, čo je proces postupne eliminujúci čísla. Na začiatku obsahuje všetky celé čísla. Opakovane sa vždy vezme najnižšie číslo na zozname (okrem 1) a eliminujú sa všetky čísla v poradí na mieste násobkov tohto čísla. Najprv sa teda odstráni každé druhé číslo, ostanú 1, 3, 5, 7, 9…, ďalšie najnižšie číslo je číslo 3, odstráni sa každé tretie číslo, vznikne množina: 1, 3, 7, 9, 13, 15… Ďalším číslom, ktoré prežilo elimináciu, je číslo 7, odstráni sa každé siedme číslo, a tak môžeme pokračovať donekonečna. Vznikne postupnosť: 1, 3, 7, 9, 13, 15, 21, 25, 31, 33, 37, 43, 49, 51, 63, 67, 69, 73, 75…
V populárnom seriáli Teória veľkého tresku postava Sheldon Cooper označuje číslo 73 ako svoje obľúbené číslo. Často mal na scéne aj tričko s vyobrazením tohto čísla. V morzeovke sa číslo 73 používa ako pozdrav na rozlúčku. Vysiela sa ako – – . . . . . . – – a je tiež palindrómom.
Kaprekarove konštanty
Indický matematik Dattatreya Ramchandra Kaprekar (1905 – 1986) sa venoval teórii čísel, objavil a podrobne popísal mnoho ich vlastností. Je po ňom pomenovaná Kaprekarova konštanta. Jej štvorciferná verzia je číslo 6 174. Keď preusporiadame číslice od najväčšej po najmenšiu, dostaneme číslo 7 641. A, naopak, usporiadaním od najmenšej po najväčšiu číslicu vznikne číslo 1 467. Keď ich od seba odpočítame, čiže 7 641 − 1 467 = 6 174, dostaneme sa naspäť k číslu 6 174.
Celý článok nájdete v časopise Quark 6/2025.
Vďaka predplatnému si ho však môžete dočítať už teraz a získať aj prístup k exkluzívnemu obsahu!
Máte predplatné?
Prihlásiť saFakulta matematiky, fyziky a informatiky
Univerzita Komenského v Bratislave



