Na názvoch záleží – niekedy aj v matematike. Ktorému bežnému smrteľníkovi sa fantázia rozbehne pri definícii φ = (1 + √5)/2 ≈ 1,618? Ak však spomeniete zlatý rez či božskú proporciu, pozornosť laikov máte zaručenú.
Zlatý rez definoval okolo roku 300 pred n. l. Euklides na základe úlohy ako rozdeliť úsečku na dve časti tak, aby pomer dĺžky dlhšej časti ku kratšej časti bol rovnaký ako pomer celej úsečky k dlhšej časti. Výsledok nazval krajný a stredný pomer, a tým sa mohol celý príbeh aj skončiť. Nebyť stredovekého matematika Leonarda z Pisy, ktorý ho oprášil o 1 500 rokov neskôr.
Od králikov po Vergília
Leonardo z Pisy, známy pod prezývkou Fibonacci (asi 1170 – 1240), bol veľkým popularizátorom indoarabských číselných zápisov (v Európe sa naďalej používali rímske číslice). Vo svojom diele Liber Abaci z roku 1202 propagoval nový systém pomocou rôznych príkladov: medzi nimi číselný rad 1, 1, 2, 3, 5, 8, 13… Fibonacci popisoval idealizovaný chov králikov; tento rad však poznali indickí matematici už v 6. storočí. Pokračuje donekonečna a čím vyššie ideme, tým viac sa pomer dvoch po sebe idúcich členov blíži k hodnote φ (≈1,618).

Fibonacci pre φ ešte nijaký názov nemal. O tristo rokov neskôr ho však matematik Luca Pacioli v diele, ktoré ilustroval Leonardo da Vinci, nazval božská proporcia (divina proportione) a zahrnul ho do teórie proporcií a polymetrickej geometrie (zobrazenia platónskych telies). Autorom názvu zlatý rez sa stal o ďalších tristo rokov Martin Ohm, nemecký matematik a mladší brat fyzika Georga Ohma, ktorý ho použil vo svojej učebnici matematiky v roku 1835.
Tam, kde renesanční umelci hľadali miery ľudských postáv či ideálnych telies, racionalisti 19. storočia nachádzali dokonalosť prírody: zlatý rez sa začal hľadať v rastlinách, ľuďoch, kameňoch aj vo vesmíre. A, samozrejme, aj v umení a architektúre (od Vergíliovej Eneidy po Veľkú pyramídu v Gíze). Mnoho mýtov o všadeprítomnosti zlatého rezu má korene práve v 19. storočí.
Všadeprítomný mýtus
Ak sa nové listy či semienka ukladajú okolo stonky pod zlatým uhlom (≈ 137,508°), vznikne najrovnomernejšie pokrytie bez opakujúcich sa línií (tzv. optimálne balenie). Je pravda, že slnečnice (často 34/55, 55/89…), šišky, ananásy, artičoky aj niektoré aloy majú opačne orientované špirálové lúče, ktorých počty sú podľa Fibonacciho čísel. V mineráloch sa φ objavuje v mierke kvázikryštálov (päťnásobné/ikosahedrické symetrie).
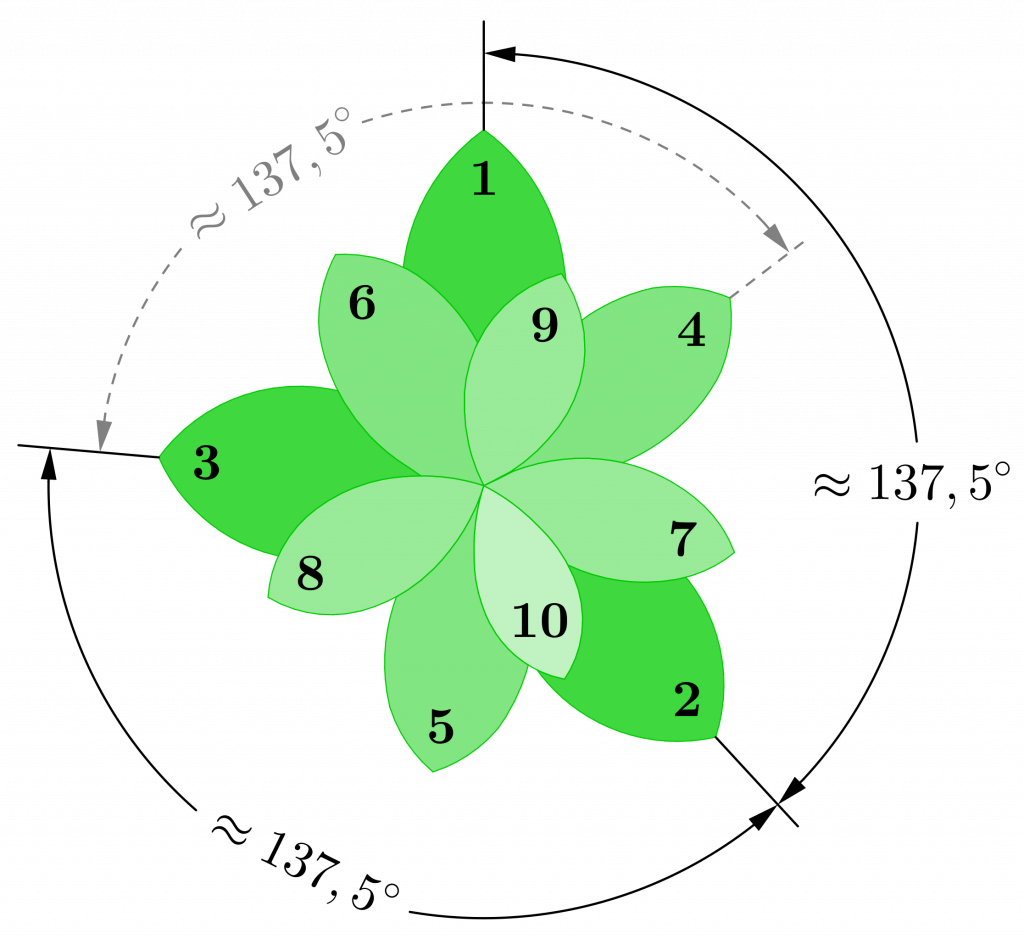
Listy však nerastú pod zlatým uhlom vždy: pre konkrétnu geometriu listov môžu iné uhly zachytiť viac svetla – preto v prírode existujú prechody a výnimky. Nesprávne interpretované sú aj tvrdenia o zlatých proporciách v lastúrach nautila, ideálnej ľudskej tvári, galaxiách či hurikánoch: ide skôr o všeobecné logaritmické špirály s rôznymi parametrami, nie špeciálne zlaté. Veľká pyramída v Gíze má pomer polovičnej základne k výške približne 1,57, čo je blízke π/2, nie φ. A pomer dĺžky stylobatu (vrchnej časti základne) k výške fasády Partenónu je asi 1 : 2,25, ďaleko od 1 : 1,618. Antickí Gréci používali racionálne pomery (1 : 2, 2 : 3, 3 : 4) a systém, ktorý umožňoval opakovať rozmery bez iracionálnych čísel. Hoci krajný a stredný pomer poznali, neexistuje dôkaz, že by ho vedome používali v staviteľstve.
Celý článok nájdete v časopise Quark 11/2025.
Vďaka predplatnému si ho však môžete dočítať už teraz a získať aj prístup k exkluzívnemu obsahu!
Máte predplatné?
Prihlásiť sa

