Zlatý rez je číslo. Je to možno sklamanie, ale tento honosný názov naozaj nesie jedno konkrétne číslo. Na to, či je toto číslo natoľko zaujímavé, že si zaslúži vlastné meno, si môže urobiť každý svoj názor.
Zlatý rez je pomerom dvoch častí úsečky, ktorá je rozdelená tak, aby platilo, že pomer dĺžky celej úsečky k jej dlhšej časti je rovnaký ako pomer dlhšej časti ku kratšej. Označme si tento pomer písmenom Φ. Teda ak máme úsečku AB, tak bod C treba na nej zvoliť tak, aby pre veľkosti úsečiek │AB│,│AC│,│BC│ platilo │AB│/│AC│= │AC│/│CB│=Φ. Ak si uvedomíme, že │AB│=│AC│+│CB│a│CB│/│AC│= 1/ Φ, tak ľahko odvodíme, že Φ=│AB│/│AC│=(│AC│+│CB│)/│AC│=│AC│/│AC│+│CB│/│AC│=1+1/Φ. To znamená, že platí Φ=1+1/Φ a po úprave dostávame kvadratickú rovnicu Φ²-Φ-1=0, ktorá je kľúčová pre rôzne vlastnosti zlatého rezu. Tejto rovnosti vyhovuje jediné kladné riešenie Φ=(1+√5)/2. Teda hľadaný pomer úsečiek je (1+√5)/2, čo sa v priebehu stáročí zvyklo označovať ako zlatý rez, božský rez, zlaté číslo alebo jednoducho fí (Φ). Pre úplnosť uveďme, že (1+√5)/2 sa približne rovná 1,618 a tento pomer nezávisí od dĺžky pôvodnej úsečky AB.
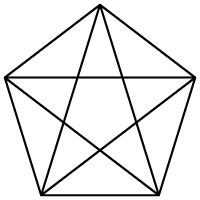
Prvý bol Pytagoras
V matematickom prostredí sa prvýkrát stretávame so zlatým rezom u Pytagora (580/572 pred n. l. – 497 pred n. l.) a jeho školy. Za svoj znak si vybrali pentagram – päťcípu hviezdu, ktorú vlastne tvoria uhlopriečky pavidelného päťuholníka. Z ich matematickej pozostalosti sa zachovalo málo, ale môžeme predpokladať, že vedeli postup konštrukcie na zostrojenie pravidelného päť- a desaťuholníka. S pravidelnými päťuholíkmi sa stretávame aj v obdobiach pred gréckou matematikou. Napríklad dodecahedron (teleso zložené z dvanástich pravidelých päťuholníkov) poznali Etruskovia už pred rokom 500 pred n. l. V týchto skorých dobách sa však pochybuje o tom, že by si ich tvorcovia uvedomovali matematické vlastnosti týchto objektov. Ukazuje sa, že uhlopriečky v pravidelnom päťuholníku sa rozdeľujú práve v pomere zlatého rezu. Vďaka tejto vlastnosti sa dá zostrojiť pravidelný päť- a desaťuholník len pomocou pravítka a kružidla. Pre úplnosť poznamenajme, že pomocou zlatého rezu sa dá presne vyjadriť aj kosínus uhla 36°, cos 36°=Φ/2=(1+√5)/4, ktorý má úzky súvis práve s pravidelným päťuholníkom. Aj Platón (okolo 428 pred n. l. – 347 pred n. l.) vo svojom spise o prírodných vedách a kozmológii Timaeus spomína zlatý rez a považuje ho za veľmi dôležitý pre matematiku a fyziku. Na základe týchto referencií dokazuje Eudoxus (408 pred n. l. – 355 pred n. l.) niekoľko viet o vlastnostiach zlatého rezu. Zhrnúc poznatky svojich predchodcov uvádza Euklides (565 pred n. l. – 300 pred n. l.) vo svojich Základoch postup konštrukcie zlatého rezu a na základe toho aj konštrukciu pravidelného päť- a desaťuholníka. V tomto období ešte neexistuje označenie zlatý rez, ani iný jednotne používaný termín. Euklides píše o zlatom reze ako o delení úsečky vo vonkajšom a vnútornom pomere.

Fibonacciho postupnosť
Ďalším dôležitým medzníkom v histórii zlatého rezu je kniha Leonarda Fibonacciho z Pisy (okolo 1170 – 1240) Liber Abaci. V nej sa autor okrem iného zaoberal reprodukciou králikov. Uvažoval o modeli králičieho páru, ktorý sa každý mesiac rozmnoží o jeden ďalší pár. Každý nový králičí pár je schopný plodiť po dvoch mesiacoch a králiky neumierajú. Výpočet množstva králičích párov vedie na postupnosť 1, 1, 2, 3, 5, 8, 13, 21, …, kde každý jej nasledujúci člen vznikne sčítaním dvoch predchádzajúcich členov. Napríklad 13=5+8, 21=13+8, ďalšie číslo bude 13+21=35 a tak ďalej. Táto postupnosť je v súčasnosti známa ako Fibonacciho postupnosť. Dá sa ukázať, že pomer dvoch po sebe idúcich členov Fibonacciho postupnosti sa bude stále viac a viac blížiť k Φ, ak budeme brať väčšie a väčšie členy (limit tohto pomeru je Φ). Túto vlastnosť nájdeme aj pri iných podobných postupnostiach, pri ktorých sa nový člen vytvorí sčítaním posledných dvoch členov, napríklad v postupnosti 3, 4, 7, 11, 18, 29, 47, … Existuje matematická teória, ktorá dáva do súvisu takéto postupnosti a riešenia kvadratických rovníc. V prípade Fibonacciho postupnosti dostaneme už známu kvadratickú rovnicu x²=x+1, ktorej riešením je číslo Φ. Tento atribút zlatého rezu však nie je až taký výnimočný, ako by sa mohlo zdať. Keby sme zvolili postupnosť s iným predpisom, napríklad 1, 1, 3, 7, 17, 41, …, ktorej ďalšie členy vznikajú sčítaním predposledného a dvojnásobku posledného člena, zistili by sme, že pomer po sebe idúcich členov sa bude blížiť k čísli 1+√2=2,414, čo je riešením kvadratickej rovnice x²=2x+1. Celkovo sa dá povedať, že existuje nekonečne veľa čísel, pre ktoré by sme dokázali nájsť postupnosť, v ktorej pomer po sebe idúcich členov sa bude blížiť práve k tomuto číslu. Je veľmi pravdepodobné, že sám Fibonacci si súvislosť medzi jeho postupnosťou a číslom Φ neuvedomoval.
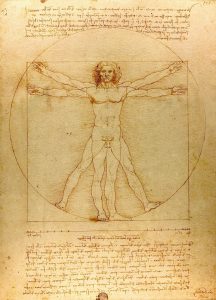
Najprv božský, potom zlatý
V období renesancie rastie záujem o zlatý rez. Jeden z najvýznamnejších matematikov svojho obdobia františkán Luca Pacioli (1445 – 1514) vydáva v roku 1509 knihu s názvom De Divina Proportione (O božskom reze), ktorú ilustroval Lonardo da Vinci (1451 – 1519). V tejto pulikácii sa číslo Φ objavuje pod pomenovaním božský rez. Prvýkrát sa názov zlatý rez, teda presnejšie goldener Schnitt, objavil v knihe Die reine Elementar-Mathematik vydanej v roku 1835. Napísal ju Martin Ohm, mladší brat fyzika Georga Simona Ohma. Až v relatívne nedávnom období, po roku 1900, použil americký matematik Mark Barr grécke písmeno Φ na označenie čísla (1+√5)/2. Urobil tak na počesť antického sochára Feidia (500 pred n. l. – 432 pred n. l.), o ktorom sa mieni, že používal zlatý rez pri tvorbe svojich sôch.

Fí priťahuje umelcov
Veľmi často sa uvádza, že umelci staroveku, renesancie a neskorších epoch používali číslo Φ pri vytváraní svojich umeleckých diel. Zvykne sa hovoriť, že pyramídy pri Gíze a chrám Parthenón v Aténach postavili tak, aby proporčne vyhovovali zlatému rezu. Keďže sa nezachovali žiadne podklady o ich stavbe, všetky tieto domnieky sa zakladajú na meraní stavieb. Tieto stavby sú pomerne zložité a dá sa na nich odmerať množstvo dĺžok. Preto medzi nimi nie je ťažké nájsť niekde presne taký pomer, aký si dopredu zvolíme. Podobne sa uvádza, že rôzni slávni maliari používali číslo Φ, aby docielili vyššiu estetičnosť svojich obrazov. V tejto súvislosti sa spomínajú Leonardo da Vinci (1451 – 1519), Michelangelo (1475 – 1564), Rafael (1483 – 1530), Rembrand (1606 – 1669), Salvador Dalí (1904 – 1989) a mnohí ďalší. Nakoľko je to odôvodnené, vedia snáď iba sami umelci. Keďže Salvador Dalí písal o svojich maľbách, dalo by sa očakávať, že sa zmieni aj o zlatom reze, ak bol preňho taký dôležitý. Túto spojitosť však maliar neuviedol. Sú však známi aj umelci, ktorí zámerne zakomponovávali číslo Φ do svojich diel. Takým bol napríklad architekt Le Corbusier (1887 – 1965), ktorý používal proporcie zlatých obdĺžnikov pri navrhovaní okien, dverí a celých budov.
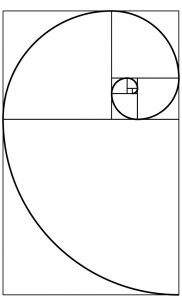
Zaujímavé vlastnosti
Zlatý rez má niekoľko ďalších zaujímavých vlastností. Platí, že √(1+√(1+√(1+√(1+ …))))=Φ, pretože riešenie tohto príkladu znova vedie k už uvedenej kvadratickej rovnici x=x²-1. Ďalej si môžeme všimnúť, že 1/Φ=0,618, teda číslo presne o jednotku menšie ako Φ. Z matematického hľadiska však nejde o žiadnu novú vlastnosť. Vyjadruje ju vlastne vzťah Φ-1=1/Φ a po jednoduchej úprave nám vyjde, že sme len inak zapísali rovnosť Φ²-Φ-1=0 uvedenú vyššie. Teda stačí si len uvedomiť pár základných súvislostí a zistíme, že zdanlivo nová vlastnosť čísla Φ, je len inak zapísaná jeho základná charakteristika, pomocou ktorej sme ho definovali. Obdĺžnik, ktorý má dĺžky strán v pomere zlatého rezu, teda a/b=Φ, sa nazýva zlatým obdĺžnikom. Dá sa dokázať, že ak zo zlatého obdĺžnika odoberieme štvorec bxb, ostane nám obdĺžnik so stranami b, a-b, ktorého dĺžky strán sú tiež v pomere zlatého rezu. Podobne môžeme z tohto novovytvoreného zlatého obdĺžnika odobrať štvorec s dĺžkou strany a-b a dostaneme ďalší zlatý obdĺžnik s pomerom strán Φ. Takýmto spôsobom sa dá vytvoriť akási špirála zlatých obdĺžnikov.
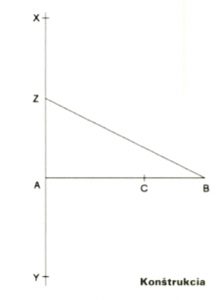
Ako sa dá skonštruovať zlatý rez?
Ako možno úsečku AB rozdeliť tak, aby pomer dĺžok jej častí bol Φ? Konštrukcia iba pomocou kružidla a pravítka je jednoduchá:
1. bodom A vedieme kolmicu na úsečku AB
2. na nej zostrojíme bod X tak, aby sa veľkosť úsečky AX rovnala veľkosti úsečky AB
3. zostrojíme bod Z ako stred úsečky AX
4. narysujeme úsečku ZB
5. na polpriamke ZA zostrojíme bod Y tak, aby sa veľkosť úsečky ZY rovnala veľkosti úsečky ZB
6. na úsečke AB zostrojíme bod C tak, aby sa veľkosť úsečky AC rovnala veľkosti úsečky AY
Pomocou Pytagorovej vety sa dá ľahko ukázať, že bod C delí úsečku AB tak, že │AB│/│AC│=│AC│/│CB│. Teda bod C delí danú úsečku v zlatom reze.
Kristína Černeková






