Dokonalé kocky

Ak ste niekedy videli hru Dungeons & Dragons, možno ste si všimli, že sa pri nej používajú zaujímavé kocky zvláštnych tvarov. Kde sa tieto kocky vzali? Súvisí s nimi nejaká zaujímavá matematika?

V matematike tieto kocky nazývame platónske telesá. Ide o mnohosteny, ktoré sú dokonale pravidelné – ich steny sú tvorené pravidelnými mnohouholníkmi, každý s tým istým počtom hrán a vrcholov, a v každom vrchole sa zbieha rovnaký počet hrán.

Platón a Kepler

Poznáme ich práve päť: štvorsten (s trojuholníkovými stenami), kocka (so štvorcovými stenami), osemsten (opäť trojuholníky), dvanásťsten (steny sú päťuholníky) a dvadsaťsten (zasa trojuholníky). Pre úplnosť dodajme, že okrem týchto kociek sa v Dungeons & Dragons používajú aj nepravidelné desaťstenné kocky.
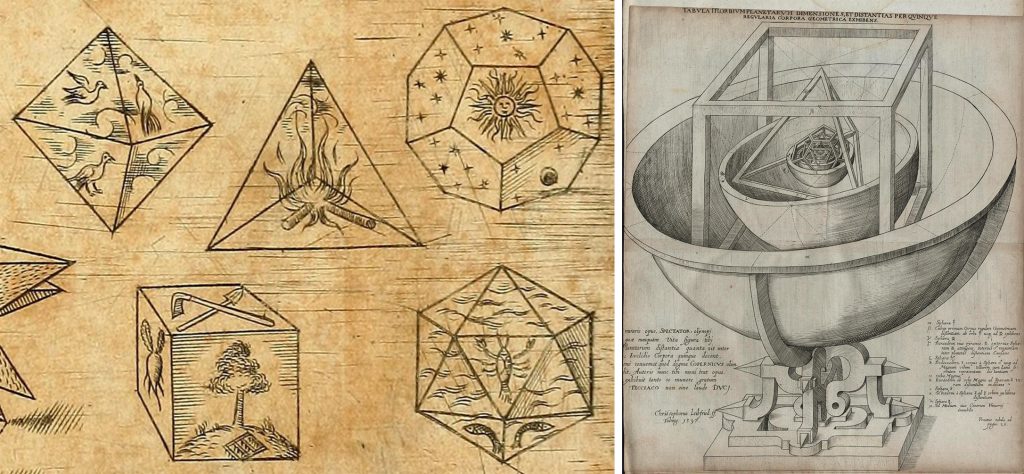
Ľudstvo sa s týmito telesami pohrávalo už oddávna. Platón vo svojom diele Timaios napríklad navrhol súvis medzi elementmi oheň-zem-vzduch-voda a štyrmi z týchto tvarov, pričom zvyšný dvanásťsten mal reprezentovať tvar vesmíru. Kepler sa zasa neskôr snažil vysvetliť usporiadanie Slnečnej sústavy postupným vkladaním platónskych telies medzi jednotlivé dráhy planét.

Prečo práve päť?

Odkiaľ vieme, že neexistuje viac takýchto pravidelných mnohostenov? Čo tak napríklad nejaké teleso so sedemuholníkovými stenami? Existuje viacero spôsobov, ako možno nahliadnuť, že náš päťčlenný zoznam je úplný. Uveďme si jeden z dôkazov, založený na tzv. Eulerovej vete, ktorá hovorí, že pre ľubovoľný mnohosten (aj nepravidelný, ale musí byť zdeformovateľný na povrch gule) platí: počet stien − počet hrán + počet vrcholov = 2.
Predpokladajme teraz, že máme nejaký dokonale pravidelný mnohosten. Keďže každá stena má rovnaký počet hrán – označme ho X – a každá hrana je spoločná práve pre dve steny, platí: (počet stien) × X = (počet hrán) × 2. Podobne, keďže v každom vrchole sa stretá rovnaký počet hrán – označme ho Y – a každá hrana sa dotýka práve dvoch vrcholov, platí: (počet vrcholov) × Y = (počet hrán) × 2. Keď si z týchto formuliek vyjadríme počty stien a vrcholov a dosadíme do Eulerovej vety, po krátkej úprave dostaneme jednoduchú rovnicu: 1/X + 1/Y = 1/2 + 1/(počet hrán).
Nezabúdajúc, že X aj Y musia byť väčšie než 2, je ľahké sa presvedčiť, že táto rovnica má celočíselné riešenia jedine v prípadoch, keď dvojica (X, Y) má hodnoty (3, 3), (3, 4), (4, 3), (3, 5) alebo (5, 3). Pri pohľade na obrázok je potom už ľahko vidieť, že týchto päť možností zodpovedá v tomto poradí presne štvorstenu, osemstenu, kocke, dvadsaťstenu a dvanásťstenu.
Dvojici (X, Y) hovoríme Schläfliho symbol. Vidíme, že riešenia sú pekne symetrické – ku každej dvojici máme aj dvojicu s prevrátenými hodnotami. V tomto prípade hovoríme, že príslušné mnohosteny sú navzájom duálne. Kocka je teda duálna osemstenu a dvanásťsten je duálny dvadsaťstenu. Štvorsten je duálny sám sebe.

Iné počty rozmerov

Čo dostaneme, ak namiesto týchto mnohostenov v troch rozmeroch skúmame zodpovedajúce objekty – nazývame ich pravidelné polytopy – v iných počtoch rozmerov? Ľahko vidíme, že úlohu platónskych telies v dvoch rozmeroch hrajú pravidelné mnohouholníky: trojuholník, štvorec, päťuholník atď. Je ich teda nekonečne mnoho. A čo vo viacerých rozmeroch? Ukazuje sa, že ak ideme do 5D a vyššie, existujú iba tri pravidelné polytopy, konkrétne viacrozmerné zovšeobecnenie štvorstenu a kocky spolu s jej duálnym osemstenom.
Situácia je však zaujímavejšia v štyroch rozmeroch, kde dostávame až šesť možností. V štyroch rozmeroch budú mať naše telesá okrem vrcholov, jednorozmerných hrán a dvojrozmerných stien aj trojrozmerné bunky. Namiesto mnohostenov je teda lepšie hovoriť o mnohobunkovcoch. Uvedených šesť riešení potom možno nazvať takto: päťbunkovec (vyššia verzia štvorstenu), osembunkovec (vyššia verzia kocky, nazývaná tiež teserakt), 16-bunkovec (vyššia verzia osemstenu), 120-bunkovec (vyššia verzia dvanásťstenu), 600-bunkovec (vyššia verzia dvadsaťstenu) a napokon 24-bunkovec, ktorý nemá trojrozmerný platónsky analóg.

Fridrich Valach
Karlova univerzita v Prahe
Viac podobných článkov nájdete na stránke vedator.space. Vedátora môžete sledovať aj prostredníctvom bezplatnej mobilnej aplikácie.