Konštanta pí, označovaná aj gréckym písmenom π, sa používa pri rôznych výpočtoch s kružnicami a označuje pomer obvodu kružnice k jej priemeru. Hodnota π je po zaokrúhlení číslo 3,14, no desatinný rozvoj čísla π je nekonečný.
Podľa definície kružnica je množina všetkých bodov, ktoré majú od daného bodu rovnakú vzdialenosť. Pojem vzdialenosť môže byť však chápaný rozlične. Štandardne pod vzdialenosťou dvoch bodov v geometrickej rovine rozumieme dĺžku úsečky spájajúcu tieto dva body, teda vzdialenosť najkratšou vzdušnou čiarou. To je tzv. euklidovská metrika, v ktorej vzdialenosť dvoch bodov vypočítame dosadením ich súradníc do vzorca. Kružnica v tejto metrike so stredom v bode (0, 0) a polomerom 1 má obvod zaokrúhlene 6,28 a priemer 2. Pomer obvodu k priemeru je 3,14 = π.
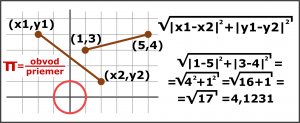
Taxikárska metrika
Ak chceme zmeniť hodnotu čísla π, musíme zmeniť spôsob merania vzdialenosti. To ovplyvní aj samotný tvar kružnice a jej obvod. Keď sa vezieme po meste taxíkom, účtovaná nikdy nie je vzdušná vzdialenosť nástupného a výstupného bodu, ale prejdená vzdialenosť po cestách. Táto myšlienka je základom tzv. taxikárskej metriky (nazývaná aj manhattanská metrika). Zidealizujme si mesto ako štvorcovú sieť ciest. Z bodu A do bodu B teraz najkratšia cesta nie je vzdušnou čiarou krížom cez budovy, ale cesta v tvare akéhosi L – najprv musíme prejsť istý počet blokov vpravo/vľavo a následne hore/dole.
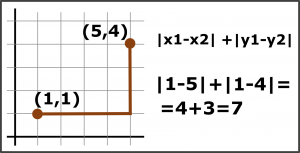
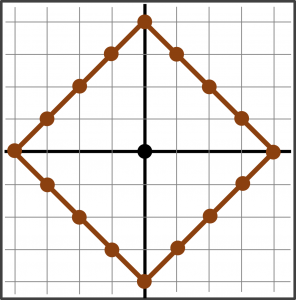
Napríklad, ak bod A má súradnice (1, 1) a bod B leží na (5, 4), tak najprv musíme z bodu A cestovať 4 bloky vpravo a následne 3 bloky hore do bodu B. Prešli sme vzdialenosť 7 blokov, čo je vzdialenosť bodov A a B v taxikárskej metrike. Mohli sme cestovať aj inou cestou, ponúka sa viacero rôznych cikcakových možností, no nikdy to nebude kratšie alebo dlhšie ako 7. Vzorec na výpočet vzdialenosti bodov v taxikárskej metrike je mierne odlišný od vzorca v euklidovskej metrike. Nakreslime kružnicu s polomerom 4 v tejto taxikárskej metrike. Pre jednoduchosť zvoľme stred v bode (0, 0) a nájdime všetky body so vzdialenosťou 4 od tohto bodu (samozrejme, nesmieme cúvať alebo sa vracať). Získame tak 16 bodov v mriežke. Matematika nemusí vždy úplne ladiť s realitou a aj v tejto metrike existujú desatinné čísla, aj keď taxík nemôže ísť 0,5 bloku vľavo a následne 3,5 bloku hore. Dôležité je najmä dodržanie pravidla pohybu iba vpravo/vľavo a hore/ dole. Po doplnení všetkých bodov vzdialenosti 4 od stredu aj s použitím desatinných čísel získame tvar diamantu. Toto je kružnica v taxikárskej metrike. Vypočítajme teraz hodnotu čísla π, pomer obvodu kružnice k jej priemeru. Priemer je viditeľne 8, z jednej strany na druhú. Priemer aj obvod musíme merať tiež taxikárskou metrikou, preto vychádza priemer 8 pre každé dva oproti ležiace body kružnice. Obvod vypočítame ako súčet dĺžok štyroch strán vzniknutého diamantu. Jedna zo strán ide z bodu (4, 0) do bodu (0, 4) a tie sú v taxikárskej metrike vzdialené 8 jednotiek. Všetky 4 strany diamantu sú rovnaké, čiže obvod má dĺžku 32 jednotiek. Obvod vydelený priemerom po výpočte vychádza π = 4.
Meranie vzdialenosti v šachu…
Taxikárska metrika má mnoho využití aj v praxi. Pri výskyte niekoľkých podobných zločinov vo veľkomeste zvyčajne páchateľ nepôsobí v blízkosti svojho bydliska, ale zároveň nezájde až príliš ďaleko. Po zakreslení lokácií zločinu na mape a vypočítaní vzdialeností práve pomocou taxikárskej metriky dosiahli kriminalisti najlepšie výsledky pri odhade bydliska páchateľa. Podobné využitia pri práci s mapami má táto metrika pri počítaní optimálnej trasy kuriérskych služieb alebo najkratšej cesty v GPS aplikáciách. Spôsobov, ako sa dá merať vzdialenosť, je omnoho viac aj v príkladoch z reálneho života a o to viac čisto vo svete matematiky. Každá figúrka v hre šach má iné pravidlá pre svoj pohyb. Pre vežu na políčku h1 je políčko h5 vzdialené iba jeden ťah. No pre kráľa na políčku h5 je políčko h1 vzdialené až štyri ťahy. Kôň umiestnený na e7 má políčko g6 vzdialené iba jeden ťah, no kráľovná potrebuje na presun z g6 na e7 dva ťahy. Tieto spôsoby merania vzdialenosti v šachu by sa tiež dali nazvať metrikami.
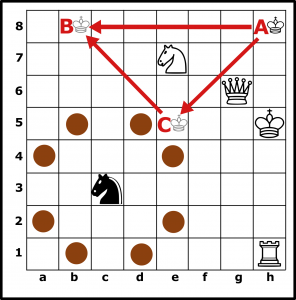
V metrike pohybu šachového koňa na políčku c3 vypočítajme hodnotu π pre kružnicu s polomerom jedného ťahu. Všetky políčka vzdialené jeden ťah koňa z c3 sú políčka b1, d1, e2, e4, d5, b5, a4, a2. Vznikne veľmi exotická kružnica. V šachu je veľmi ťažké predstaviť si desatinné hodnoty ťahov, preto ich v tomto príklade nebudeme uvažovať. Priemer kružnice bude 2, keďže každé dva oproti ležiace body sú vzdialené 2 ťahy. Obvod kružnice musíme odmerať taktiež pomocou ťahov koňa. Medzi susednými políčkami kružnice b1 a d1 prejdeme na dva ťahy a rovnako to je aj pri všetkých nasledujúcich políčkach dookola celého obvodu. To vychádza 16 ťahov koňa po celom obvode kružnice. V prípade šachovej metriky koňa pre kružnicu s priemerom dva ťahy bude hodnota π = 8. Pohyb šachových figúrok obsahuje jednu peknú anomáliu. V štandardnej euklidovskej metrike pre ľubovoľné body A, B, C platí, že ak sa body nerovnajú a neležia na jednej priamke, tak vzdialenosť z A do B je vždy menšia ako vzdialenosť z A do C spočítaná so vzdialenosťou z C do B. Podobný prípad na šachovnici v metrike figúrky kráľa dopadne inak. Cesta z políčka h8 na políčko b8 predstavuje pre kráľa šesť ťahov. Ak pridáme do trasy tretí bod ležiaci mimo spojnice h8 a b8, a to políčko e5, cez ktoré kráľ musí tiež prejsť, kráľ to zvládne tiež na šesť ťahov. Cesta obchádzkou je pre kráľa rovnako dlhá ako priama cesta.
… a na zakrivenom priestore
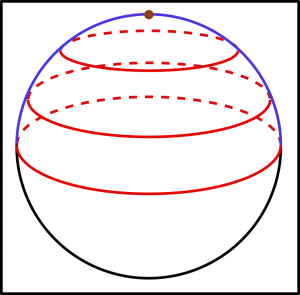
Úplne inak fungujú metriky aj na zakrivených priestoroch. Hodnota čísla π závisí od polomeru kružnice a často aj od jej umiestnenia. Jeden z najjednoduchších zakrivených priestorov je povrch gule. Kružnica umiestnená presne na rovnobežke nemá stred vnútri v strede gule, pretože berieme do úvahy iba dvojrozmerný zakrivený priestor povrchu gule. Stred takejto kružnice sa nachádza hore na severnom póle. Nezáleží na konkrétnej hodnote obvodu kružnice na rovníku, jej priemer sa bude vždy rovnať polovici jej dĺžky, pretože vzdialenosť každých dvoch bodov oproti sebe musíme merať po oblúku cez stred z jednej strany na druhú, čo je presne polkružnica s rovnakým polomerom ako pôvodná kružnica. Hodnota π sa bude v tomto prípade rovnať číslu 2. Keď túto kružnicu na guľovej ploche zmenšíme, ale zachováme jej stred na severnom póle, akoby sa posunula bližšie k pólu. Výpočet čísla π je trochu komplikovanejší. Treba si uvedomiť, že keby sme postupne zmenšovali kružnicu, tak jej celková vnútorná plocha bude čoraz menej zakrivená. Až nakoniec malá kružnica veľmi blízko stredu na severnom póle bude celá ležať na takmer rovnej ploche. A hodnota π pre kružnice na rovnej ploche je 3,14. Z toho sa dá predpokladať, že postupným zmenšovaním kružnice by sa hodnota π menila od hodnoty 2 pre kružnicu na rovníku až limitne po štandardnú hodnotu π pre nekonečne malú kružnicu na guľovej ploche.
Text a foto Stanislav Griguš
Fakulta matematiky, fyziky a informatiky
Univerzita Komenského v Bratislave
Videá autora nájdete na YouTube kanáli To ako prečo?.
