V matematických príkladoch, najčastejšie v geometrii, sa stretávame s rôzne dlhými šípkami smerujúcimi do všetkých strán. Takáto šípka sa nazýva vektor, prípadne aj orientovaná úsečka. Využíva sa nielen v zadaniach príkladov počas štúdia matematiky.
Na vysvetlenie podstaty vektorov budeme potrebovať štandardnú štvorcovú sieť so súradnicami. Bod v strede bude mať súradnice (0, 0) a následne na horizontálnej osi, nazývanej aj ako os x, bude prvá súradnica pribúdať smerom vpravo a ubúdať smerom vľavo. Rovnako druhá súradnica bude po vertikálnej osi, nazývanej aj os y, pribúdať smerom hore a ubúdať smerom dole. Na zjednodušenie budeme používať iba celé čísla súradníc bodov.
Pytagorova veta
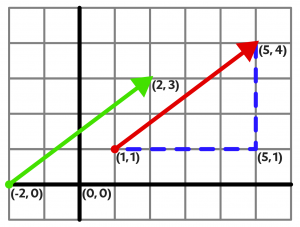
Vektor je definovaný dvomi bodmi, začiatočným a koncovým. Tieto dva body určia jeho veľkosť a smer. Napríklad vektor začínajúci sa v bode (1, 1) a končiaci v bode (5, 4) bude smerovať vpravo hore. Dĺžku (označuje sa aj ako veľkosť) vektora vieme vypočítať pomocou Pytagorovej vety. Vektor môžeme považovať za preponu pravouhlého trojuholníka a zvyšné dve strany trojuholníka doplníme na štvorcovej sieti. Strana vzniknutého trojuholníka v smere osi x má dĺžku 4, strana v smere y dĺžku 3. Dĺžku prepony teraz vypočítame ako odmocninu zo súčtu druhých mocnín dĺžok zvyšných dvoch strán trojuholníka. Tri na druhú je 9, štyri na druhú je 16. Súčet je 25 a odmocnina z 25 je pekné celé číslo 5. To je Pytagorova veta.
Na zjednodušenie počítania môžeme tento vektor posunúť do stredu súradnicovej sústavy do bodu (0, 0). Ak náš vektor označíme písmenkom v, môžeme ho zapísať aj ako v = [4, 3]. Zapísané sú súradnice bodu, do ktorého smeruje po presunutí. Presúvaním vektorov sa ich vlastnosti nijako nemenia. Graficky sa ešte zvykne pri zapisovaní vektorov pridať nad písmenko v malá šípka smerujúca vpravo.
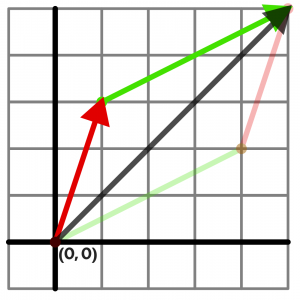
Vektor môžeme skalárne násobiť celým číslom. Jeho skalárny súčin napríklad s číslom 3 bude 3 . v, pričom stačí každú súradnicu vektora vynásobiť daným číslom. Vznikne nový vektor u = [12, 9]. Skalárnym súčinom vektora s číslom sa nezmení jeho smer, zmení sa iba jeho veľkosť. Dva vektory môžeme jednoducho sčítať tak, že sčítame osobitne každú ich súradnicu. Grafické znázornenie súčtu vektorov zodpovedá uhlopriečke rovnobežníka vytvoreného týmito dvomi vektormi.
Podobnosť
No s vektormi je možné narábať aj trochu zložitejšie. Výsledkom skalárneho súčinu dvoch vektorov nie je nový vektor, ale jedno číslo. Dva vektory skalárne vynásobíme tak, že sčítame násobky ich súradníc. Napríklad ak máme vektor a = [2, 4] a vektor b = [3, 5], prvú súradnicu vektora a vynásobíme prvou súradnicou vektora b, rovnako druhé súradnice a tieto čísla sčítame. Ich skalárny súčin teda bude (2 × 3) + (4 × 5) = 6 + 20 = 26. Skalárny súčin sa označuje bodkou, takže a . b = 26. Z neho dokážeme vyčítať rôzne vlastnosti vektorov. Napríklad ak sa skalárny súčin dvoch vektorov rovná nule, znamená to, že sú na seba kolmé. A všeobecne aj dokážeme posúdiť, aký uhol zvierajú.
Prichádza jeden zložitejší vzorec. Kosínus uhla dvoch vektorov sa rovná ich skalárnemu súčinu vydelenému súčinom ich veľkostí. Veľkosť vektora, ktorú sme si spomínali na začiatku, sa označuje dvomi zvislými čiarami pred a za písmenkom vektora. Vypočítaný vektor v úvode článku bude mať veľkosť |v| = 5.
Existuje ešte aj vektorový súčin vektorov, ktorý má zložitejší výpočet, a ďalšie matematické operácie s vektormi, dôležité pri aplikácii v reálnom živote. Jedna z najčastejších potrebných vlastností dvoch vektorov je ich podobnosť, teda aký je už spomínaný uhol vektorov, aká blízka je ich veľkosť, ich umiestnenie v súradnicovej sústave atď. Tieto vlastnosti vieme vypočítať cez matematické operácie s vektormi.
Text a ilustrácie Stanislav Griguš
Fakulta matematiky, fyziky a informatiky
Univerzita Komenského v Bratislave
Videá autora nájdete na YouTube kanáli bit.ly/ToAkoPreco.
